Arithmétique et géométrie
L’éducation a été complexifiée bien avant que nous n’ayons plus la possibilité d’évoluer de soi-même par l’école. Pour que la population accepte l’impensable on peut expliquer l’expérience de la grenouille et de l’eau bouillante. La grenouille ne se rend pas compte qu’elle peut mourir que si l’on ne chauffe l’eau que petit à petit.
De même si l’on n’applique pas un cours dans son quotidien on n’évolue pas grâce à ce cours. Alors l’école n’a plus son rôle moteur d’ascension morale, valorisant notre envie de construire pour nous permettre d’évoluer. Évoluer par l’écriture permet pourtant de mieux comprendre les autres en se comprenant soi. Pourtant quiconque a cette envie de construire en lui parce que nous sommes mus par l’envie de résoudre quoi que ce soit.
C’est lorsqu’un professeur est exigeant et pédagogue qu’il obtient le meilleur de ses élèves. Or le bon élève devient un peu un robot, car il répète la même méthode pour apprendre, alors qu’il peut y avoir plein de façons de comprendre un exercice. La géométrie permet d’en trouver beaucoup.
Quiconque peut devenir passionné, pour comprendre comment fonctionne notre société, afin de l’améliorer. La passion consiste à canaliser une envie forte pour réaliser quelque chose. La réalisation devient alors un jeu.
Seulement le cours magistral nous empêche de suffisamment s’engager vers cette culture classique de la beauté. Ainsi l’arithmétique a remplacé en grande partie la géométrie. Cela fait que les sciences sont déconnectées du réel, car une formule mathématique doit être vérifiée physiquement pour être ajoutée dans une hypothèse scientifique.
La géométrie permettrait de réduire fortement la durée des cours tout en permettant un meilleur épanouissement de l’élève. La formule (a+b)(a+b)=a2+b2+2ab peut être facilement démontrée géométriquement. L’autre exemple est celui de GAUSS et une de ses formules toujours non démontrée mais fonctionnelle. Les scientifiques ont du mal à démontrer de nouveau cette formule vraie.
-
- Un théorème démontré par la géométrie
En plus, la géométrie qui est apprise à l’école est euclidienne. Ce genre de cours débute en général en disant que la droite ne peut pas se couper elle-même. Aussi la droite ne peut exister dans le monde réel puisqu’il n’y a pas de surface avec. Difficile à l’élève de se représenter ce genre d’éléments.
Il y a pourtant mieux que la géométrie euclidienne. C’est la géométrie constructive. Elle consiste à partir d’une forme pour en construire d’autres. Avec ce genre de géométrie on peut se faciliter la compréhension d’un exercice. On peut aussi prouver des théorèmes. On pourrait même comprendre la matière en infiniment petit.
Si, comme BEETHOVEN, qui a écrit ses meilleures partitions en étant sourd, nous faisons abstraction de nos sens pour exprimer la beauté permettant notre éveil, nous pouvons être fier de notre esprit. Aussi nous devenons responsables de l’amélioration de notre civilisation. Cela fait évoluer. Cela permet notre éternité.
Pour aller plus loin les courbes et les zones représentant des équations ou inéquations linéaires nous font croire, soit que le monde se comprend en deux dimensions, soit que l’on ne peut pas résoudre certains problèmes. Ça ne fait pas travailler l’imagination.
Il existe pourtant la possibilité de comprendre plus facilement l’infini et notre économie avec des spirales logarithmiques. Ces spirales peuvent facilement faire comprendre l’évolution démographique dans le temps grâce à la science. Une explication de cette spirale logarithmique est dans la méthode Larouche-Riemann, disponible sur Internet.
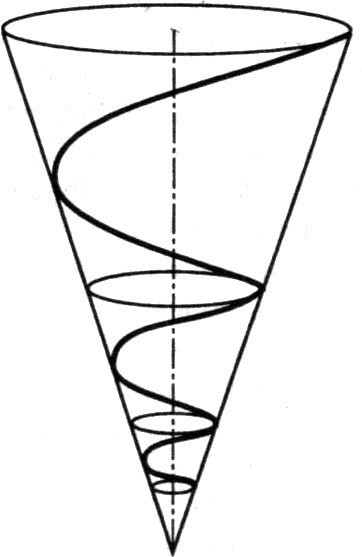
- Action conique auto-similaire
- Le cône représente l’évolution démographique idéale. Les cercles représentent les bons technologiques. La spirale représente la densité de flux d’énergie.
Vous la trouverez peut-être dans certains livres d’économie. Cette spirale utilise 3 dimensions. Cela permet de mieux comprendre certains paramètres de l’économie, basés sur la démographie, c’est à dire le cône, la création d’énergie avec la spirale intérieure. L’exemple ci-dessus est l’évolution d’un monde évoluant correctement en société, un monde démocratique et républicain où les citoyens agissent.
Sources
18 réactions à cet article
-
J’avais oublié de relater certaines choses :
http://www.devenircreatif.com/Arithmetique-et-geometrie -
C’est pas Lyndon Larouche qui fait de l’économie à partir de la physique riemanienne ?
-
ah si j’avais pas lu l’article jusqu’à la fin, ça m’apprendra...
-
bonjour
Exposé très intéressant . Dans la même veine le livre déjà ancien de Marco Wolf « la bosse des maths est elle une maladie » où l auteur expose l ensemble des mathématiques suffisantes pour un non mathématicien de profession , c est à dire tout individu cultivé qui a besoin de comprendre et d utiliser les outils mathématiques dans la vie courante.
-
L’explication de la formule du carré de a+b serait plus claire
si a2 et b2 étaient sur la même diagonale.-
-
@pissefroid
Oui, en effet.Il existe une démonstration similaire du théorème de Pythagore.-
@l’auteurL’autre exemple est celui de GAUSS et une de ses formules toujours non démontrée mais fonctionnelle.C’est quoi cette formule de Gauss non démontrée ?-
Je ne sais plus. Mais il y a bien une formule de Gauss non démontrée et fonctionnelle.
-
Tout irait bien, si le schéma... n’était pas faux !
La vrai schéma serait celui-ci (j’ai dû utiliser les « - » à la place des blancs) :
------a------b
---_________
—|--------|-------|
a-| a²-----|ab---|
—|_____|-___|
b-|ab-----|b²----|
—|_____|-___|
Sans quoi on ne comprend rien.Je n’ai pas lu le reste...
-
Désolé, la photo a tout chamboulé... Merci AV (On ne "prévisualise pas l’aspect réel, et les blancs du schéma disparaissent) !
-
-
-
-
-
-Le vrai schéma serait celui-ci (j’ai dû utiliser les « - » à la place des blancs) :
-
------a------b
---_________
—|--------|-------|
a-| a²-----|ab---|
—|_____|-___|
b-|ab-----|b²----|
—|_____|-___|
Sans quoi on ne comprend rien.Je n’ai pas lu le reste...
-
@Jean-Paul FoscarvelC’est la même remarque qu’a fait Pissefroid ci-dessus. -
^La géométrie permettrait de réduire fortement la durée des cours tout en permettant un meilleur épanouissement de l’élève. La formule (a+b)(a+b)=a2+b2+2ab peut être facilement démontrée géométriquement.
Ce n’est qu’un cas particulier de la formule du binôme de Newton avec N=2.
Sauf qu’on veut mettre la charrue avant les bœufs en France : on apprend à développer (a+b)² en quatrième puis (a+b)^3 en seconde, en terminale on voit la formule (il y a aussi le triangle de Pascal mais je sais pas si c’est au programme) et c’est dans le supérieur qu’on apprend à démontrer cette formule (démonstration par récurrence).Des collégiens peuvent comprendre le raisonnement par récurrence...si on les initiait à l’informatique plus jeune...
-
-
-
Hello,
Le problème avec la « géométrie » telle que vous l’utilisez, c’est qu’elle remplace la démonstration par l’intuition. Et l’intuition peut très facilement être mise en défaut.
http://fr.wikipedia.org/wiki/Paradoxe_du_carr%C3%A9_manquant
Je suis d’accord toutefois que ça aide à la compréhension d’un mécanisme, et fournit une bonne mnémotechnie.
-
Moi aussi je vais faire de la pub pour une pédagogie associant géométrie et arithmétique :
avec le projet Gam1 vous pouvez tout aussi bien :- démontrer le théorème des Potinus de Pythagore ...
- aligner des intersections
- évaluer la dangerosité des Sievert ...
- et bien d’autres choses encore comme ... calculer/comparer vos impôts ... jouer au pendu ... faire de la divination ... ou des dessins animés ...
-
« ...La formule (a+b)(a+b)=a2+b2+2ab peut être facilement démontrée géométriquement ».
Et l’élève studieux, ne posera jamais la bonne question. Il ira chercher la bonne note et sera heureux avec son 16/20.
L’autre élève studieux aura un 6/20, imbécile qu’il est, à se triturer le cerveau en cherchant la réponse à cette bonne question qu’il n’a pas osé poser. Heureusement car le prof n’a pas de réponse.
Le studieux, avec son 16/20 deviendra quelqu’un...Il dessinera un cône, des cercles, une spirale et déclarera devant ses compères ébahis : « C’est l’évolution de l’humanité. C’est l’évolution d’un monde évoluant correctement(?) en société ».
Applaudissements, reconnaissance, interview...politiques monétaires, alimentaires, gestion des énergies, flux de capitaux, courbe du chômage et de la croissance. Encore un expert !!!Un petit coup de milliards pour éblouir ; rapidement transformés en pourcentage pour masquer les défaut, les lacunes, les dégâts collatéraux.
Et le pauvre imbécile, qui se pose encore la bonne question : « Ca sert à quoi ?
- Mais, c’est toi qui ne sert à rien, tu n’es personne, juste une variable d’ajustement. »
Et toujours pas de réponse.
Prenons les maths pour ce qu’ils sont, un langage parmi d’autres. Utile quand on sait le maîtrisé, dangereux quand on en abuse. On vit très bien avec, et beaucoup réalisent de belles choses en utilisant leurs énergies, leurs découvertes, leurs évolutions sans jamais utiliser ou même connaître ce langage.
La vie n’est pas mathématique. Elle n’entre pas dans un cône.
-
-
-
-
-
-
-
-
-
Ajouter une réaction
Pour réagir, identifiez-vous avec votre login / mot de passe, en haut à droite de cette page
Si vous n'avez pas de login / mot de passe, vous devez vous inscrire ici.
FAIRE UN DON
